Soon after the Udacity author finishes Bayes, he extends it to Naive Bayes, and since our approach is different, now we need to understand the same via our lens once again.

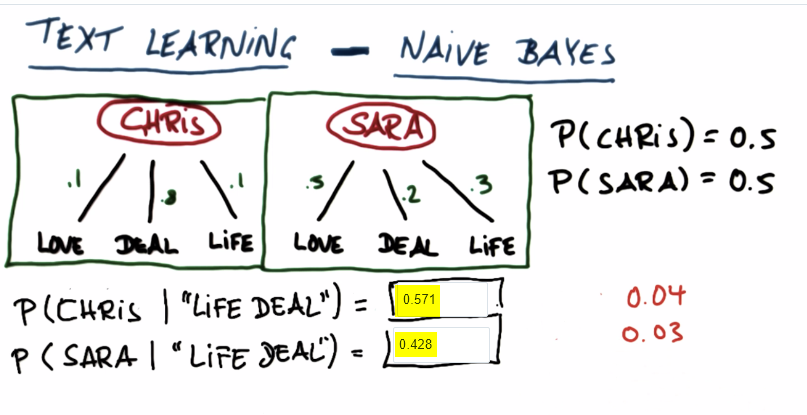
Problem: We need to find out who probably sent the mail among Chris and Sara, provided a pattern observed in the mail. For brevity, we consider only 3 words, and assume the following.

1. Chris and Sara sending email are mutually exclusive. Its either Chris or Sara, never both and they both have equal chance
2. The 3 words (Love, Deal, Life) from them have following probabilities. Note these are not mutually exclusive but independent.

Chris: Love (0.1), Deal (0.8), Life (0.1)

Sara:  Love (0.5), Deal (0.2), Life (0.3)

What is the probability that mail came from Chris, given the words "Life and Deal"? Similarly find for Sara as well.

Our tree diagram would be as follows initially.

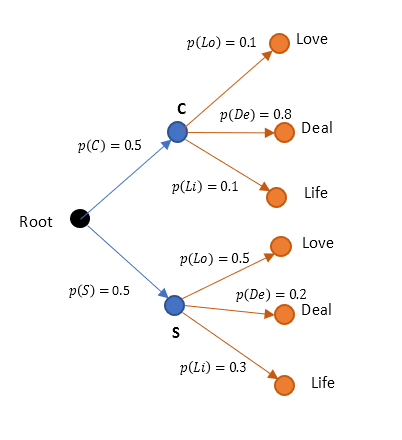
Earlier I said, the probabilities of branches from a node add up to 1. Sorry, it was not always the case. For events that are mutually exclusive, this could be true but which are independent of each other, it need not be. This distinction would help us solve this puzzle, because, in above case, blue nodes (Chris/Sara) are mutually exclusive while orange (words), are independent of each other. I also would like to use an alternate notation.

p(A and B) can also be represented and for better understanding as $ p(\text {A} \cap \text{B})$. Similarly p(A or B), which means probability of A or B or both, can be represented as $ p(\text {A} \cup \text{B})$

As per basic probability summation rule for two events A and B,

$ p(\text {A} \cup \text{B}) = p(\text{A}) + p(\text{B}) - p(\text {A} \cap \text{B})$(1)

Now for mutually exclusive events, they both can't happen together. Thus

$ p(\text {A} \cap \text{B}) = 0$(2)

For independent events, since they do not influence each other,

$ p(\text {A} \cap \text{B}) \neq 0$(3)

Rather, from earlier Bayes theorem,

$ p(\text {A} \cap \text{B}) = p(\text{A}) p(\text {B} \mid \text {A}) $(4)

Since A and B are independent,

$ p(\text {B} \mid \text {A}) = p(\text{B}) $(5)

Thus,

$ p(\text {A} \cap \text{B}) = p(\text{A}) p(\text {B}) $(6)

In terms of our problem, we could thus say from (1) and (2), as Chris and Sara are mutually exclusive,

$ p(\text {C} \cap \text{S}) = 0\\ p(\text {C} \cup \text{S}) = p(\text{C}) + p(\text{S}) $(7)

Similarly, since words are independent of each other, for "Life and Deal", we could say, from (1) and (6),

$ p(\text {Li} \cap \text{De}) = p(\text{Li}) p(\text{De}) \\ p(\text {Li} \cup \text{De}) = p(\text{Li}) + p(\text{De}) - p(\text {Li} \cap \text{De}) \\ p(\text {Li} \cup \text{De}) = p(\text{Li}) + p(\text{De}) - p(\text{Li})p(\text{De}) $(8)

Applying p(Li ∩ De) = p(Li)p(De) in our tree we could condense it further as below.

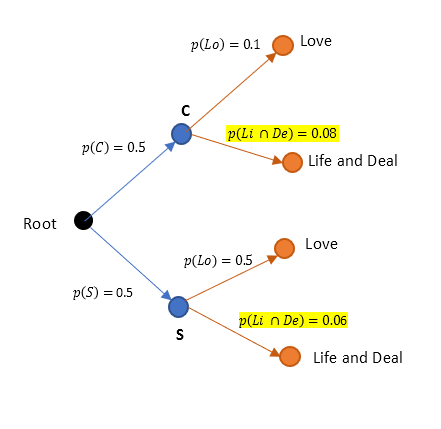
Now our problem becomes simpler to tackle. We just need to find p(C | Li ∩ De) and p(S | Li ∩ De)

From Figure 2, we can deduce p( C ∩ (Li ∩ De)) as below

$ p(\text {C} \cap \text {Li} \cap \text{De}) = (0.5)(0.08) = 0.04$(9)

Also for p( S ∩ (Li ∩ De))..

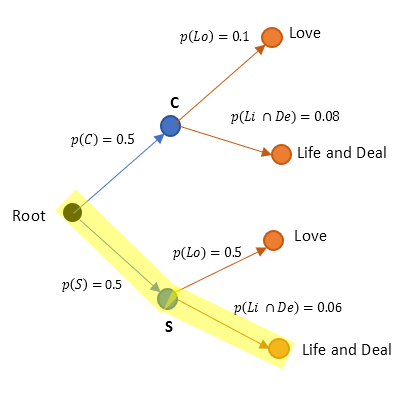
$ p(\text {S} \cap \text {Li} \cap \text{De}) = (0.5)(0.06) = 0.03$(10)

Further, p(Li ∩ De)..

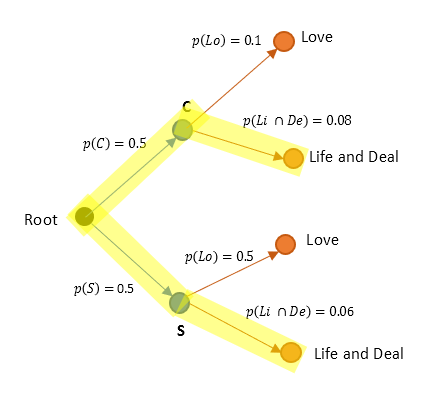
$ p(\text {Li} \cap \text{De}) = p(\text {C} \cap \text {Li} \cap \text{De}) + p(\text {S} \cap \text {Li} \cap \text{De}) = (0.5)(0.08) + (0.5)(0.06) = 0.07$
(11)

Applying (9), (10), (11), via Bayes theorem, we get the required probabilities as below.

$ p(\text{C} \mid \text{Li} \cap \text{De})=\frac{p(\text {C} \cap \text {Li} \cap \text{De})}{p(\text {Li} \cap \text{De})} = \frac{0.04}{0.07} = 0.571$(12)

$ p(\text{S} \mid \text{Li} \cap \text{De})=\frac{p(\text {S} \cap \text {Li} \cap \text{De})}{p(\text {Li} \cap \text{De})} = \frac{0.03}{0.07} = 0.428$(13)

Thus we have arrived at the answers via our lens. This also conforms with what is arrived in Udacity. :)

Note that the answer shown in Udacity are shown in shorter steps, but it is important to intuitively understand how do we do them that is why I showed step by step in detail. This way, further lectures in Bayesian domain would be now easier to comprehend.

To justify the title (though focus here is to unravel the Udacity's lecture), Naive in Naive Bayes is that we simply assumed the words outcomes are independent of each other. This is why we just have to multiply their probabilities to arrive at a conclusion. If we are to assume they are dependent, things get complicated even with just 2 or 3 words. We are learning this to deploy on 1000s of words as part of machine learning, so we accept this disadvantage as long as its reasonable to assume the words are independent in given problem.

In above problem, the labels are Chris and Sara (which we had to find out who likely sent mail given the words), and feature lists are the words.